Progressions
Sample Test
Key questions:
- What is an arithmetic/geometric progression?
- What are the main properties of progressions?
- How are progressions related to annuity and differentiated payments?
Progressions
| Practice | Achieved level |
|---|---|
| Mathematical foundations |
- Give an example of 6 numbers forming a geometric progression. How can their sum be found?
- State the characteristic property for three consecutive terms of an arithmetic progression.
How can this property be used to check whether the four numbers 15, 19, 23, 29 form an arithmetic progression? - Describe in your own words how a loan repayment scheme with differentiated payments works. How does it differ from the annuity scheme?
- A geometric progression consists of the following elements: \(1, 2, \ldots, 4096 \). Find the product of these numbers.
| Practice | Achieved level |
|---|---|
| Problem solving |
- A tourist travels from one city to another, each day covering the same additional distance compared to the previous day. It is known that on the first day the tourist walked 10 kilometers. Determine how many kilometers the tourist walked on the third day if the entire journey took 6 days and the distance between the cities is 120 kilometers.
- It is known that the numbers \( x - 16, x, 72 \) form a geometric progression. Find the smallest of them.
- Find the common difference of an arithmetic progression whose eighth term is 38 and the sum of the second and sixth terms is 36.
- Sergey took a bank loan of 1,000,000 for a period of 9 months. At the end of each month, the total remaining debt increases by 12%, and then decreases by the amount paid by Sergey. The payments made at the end of each month are chosen so that the debt decreases by the same amount each time. What percentage of the loan amount is the total amount paid by Sergey to the bank in excess of the principal?
Annuity Payments
Key Questions:
- How is a loan repaid using annuity payments?
- Which repayment scheme is more выгодна?
- How are annuity payments related to a geometric progression?
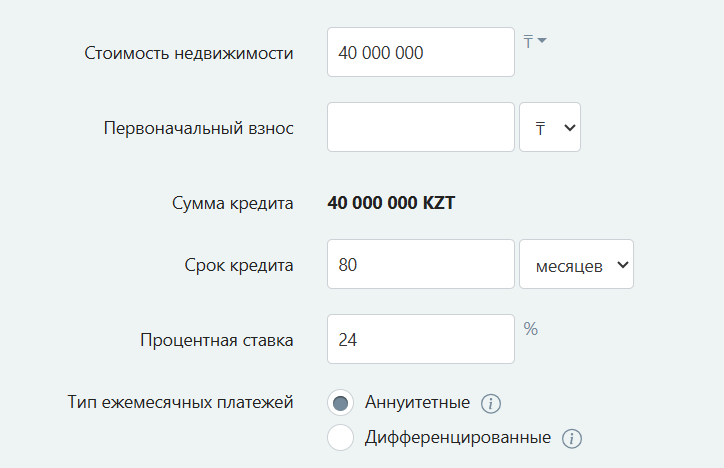
What do you see in this picture?
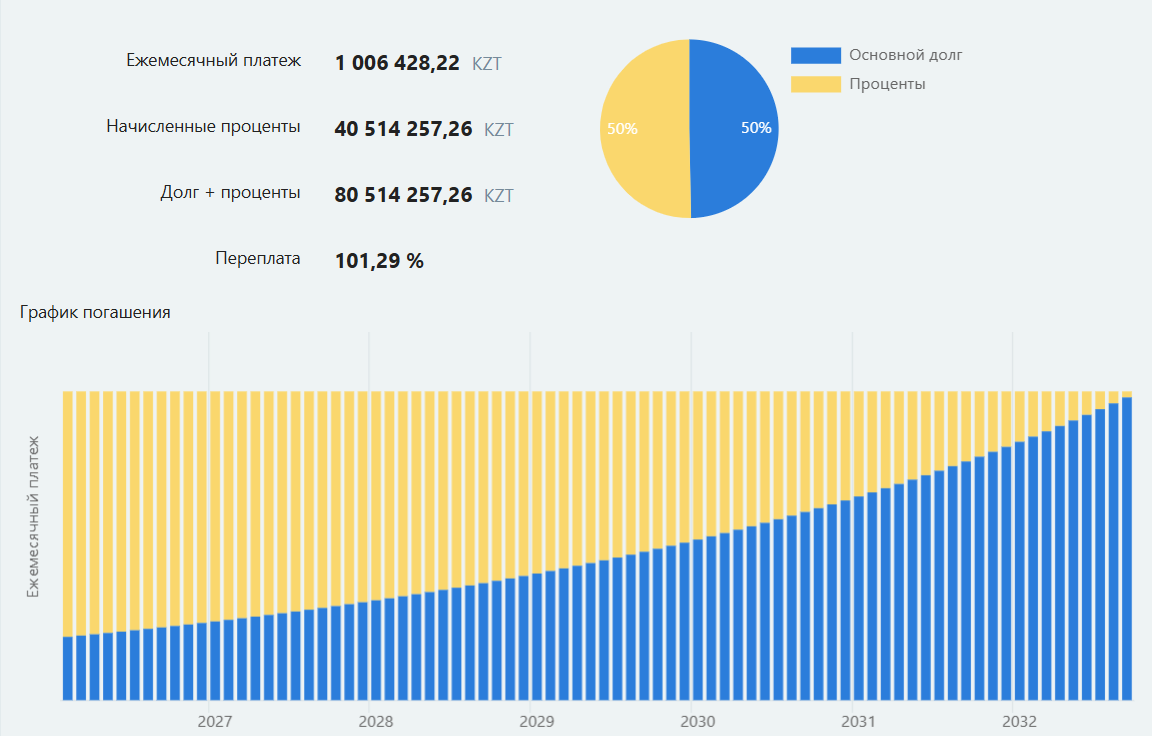
What might be the terms of this contract?
Annuity Scheme
Under an annuity repayment scheme, the borrower pays the same amount in each period.
However, the structure of the payment changes:
- at the beginning of the term, most of the payment goes to interest;
- toward the end of the term, most goes to repaying the principal.
The payment amount is chosen so that the loan is fully repaid by the end of the term.
Example
Loan amount: 331 000
Term: 3 months
Interest rate: 10% per month
Monthly payment: 133 100
| Period | Remaining debt |
Accrued interest |
Principal repaid |
Payment for the period |
|---|---|---|---|---|
| 1 | 331 000 | 33 100 | 100 000 | 133 100 |
| 2 | 231 000 | 23 100 | 110 000 | 133 100 |
| 3 | 121 000 | 12 100 | 121 000 | 133 100 |
Note that the numbers in the “Principal repaid” column form a geometric progression:
\[ 100\,000,\quad 110\,000,\quad 121\,000. \]
Payment Amount
Let the loan amount be \( S \), the interest rate per period be \( r \), the number of periods be \( n \), and the payment amount be \( A \).
For convenience in calculations, introduce the growth factor:
\[ k = 1 + \frac{r}{100}. \]
After interest is applied in the first period, the debt becomes \( kS \), and after the first payment it becomes \( kS - A \).
In the second period, the debt again increases by a factor of \( k \): \[ k(kS - A) = k^2S - kA, \] and after the second payment becomes \[ k^2S - kA - A. \]
Continuing this process, we find that before the last payment the debt equals \[ k^n S - k^{n-1}A - k^{n-2}A - \ldots - kA, \]
and after the final payment the loan must be fully repaid. Therefore, \[ k^n S - A\left(k^{n-1} + k^{n-2} + \ldots + 1\right) = 0. \]
The sum in parentheses is the sum of a geometric progression: \[ k^{n-1} + k^{n-2} + \ldots + 1 = \frac{k^n - 1}{k - 1}. \]
Substituting this expression, we obtain the equation: \[ k^n S - A \cdot \frac{k^n - 1}{k - 1} = 0. \]
Hence, the annuity payment amount is: \[ \boxed{ A = S \cdot \frac{k^n (k - 1)}{k^n - 1} } \]
ANNUITY PAYMENTS: PRACTICE
- On December 31, 2013, Sergey took a bank loan of 9,930,000 rubles at 10% per year. The repayment scheme is as follows: on December 31 of each following year the bank adds interest to the remaining debt (that is, increases the debt by 10%), after which Sergey makes an annual payment. What should the annual payment be so that Sergey repays the loan in three equal annual payments?
- In July 2018, it is planned to take a bank loan. The repayment conditions are as follows:
— every January the debt increases by 20% compared to the end of the previous year;
— from February to June each year, part of the debt must be paid in a single payment.
How many rubles should be borrowed if it is known that the loan will be fully
repaid in four equal payments and the bank will receive 311,040 rubles?
- On December 31, 2014, Timofey took a bank loan of 7,007,000 at 20% per year. The repayment scheme is as follows: on December 31 of each following year the bank adds interest to the remaining debt (that is, increases the debt by 20%), after which Timofey makes a payment. Timofey repaid the entire loan in 3 equal payments. How many rubles less would he have paid the bank if he had managed to repay the loan in 2 equal payments?
-
In July 2016, it is planned to take a loan of 4.2 million rubles. The repayment conditions are:
— every January the debt increases by r% compared to the end of the previous year;
— from February to June part of the debt must be paid;
— in July 2017, 2018, and 2019 the debt remains equal to 4.2 million rubles;
— the payments in 2020 and 2021 are equal;
Find r if in 2021 the debt will be fully repaid and the total payments amount to 6.1 million rubles.
- 3,993,000.
- 201,300 rubles.
- 806,400.
- 10.
Exit Ticket
An amount of $10,000 is issued as a loan for 6 months at 12% per year with annuity payments. Find the monthly payment amount.
Sum of a Geometric Progression
Key questions:
- What property do three consecutive terms have?
- Which method allows one to quickly compute the sum of consecutive terms?
- How can a progression be reconstructed using equations?
Warm-up
Find the sum of the numbers \( 1 + 3 + 3^2 + 3^3 + \ldots + 3^{100}\).
Characteristic property of a geometric progression
Three consecutive terms of a geometric progression have an important property: the square of the middle term is equal to the product of the two neighboring terms.
\[ a_k^2 = a_{k-1} \cdot a_{k+1}. \]
This property makes it possible to set up equations and reconstruct elements of a geometric progression from incomplete data.
Subtraction method
To derive the formula for the sum of the first \(n\) terms of a geometric progression, the subtraction method is used.
Consider the sum
\[ S_n = a_1 + a_1q + a_1q^2 + \ldots + a_1q^{n-1}. \]
Multiply this equality by the common ratio \(q\):
\[ qS_n = a_1q + a_1q^2 + \ldots + a_1q^{n}. \]
Subtract the second equality from the first one. Most terms cancel out, and only the extreme terms remain.
Formula for the sum of a geometric progression
As a result of the subtraction, we obtain:
\[ S_n (1 - q) = a_1 (1 - q^n). \]
If \( q \neq 1 \), the sum of the first \(n\) terms of a geometric progression is computed using the formula:
\[ S_n = \frac{a_1 (1 - q^n)}{1 - q}. \]
This formula is especially convenient when working with large powers and allows one to quickly find the sums of long geometric series.
Example
Let us find the sum of the first eight terms of a geometric progression, if it is known that \( a_1 = 2 \) and \( q = 3 \).
Use the sum formula:
\[ S_8 = \frac{2(1 - 3^8)}{1 - 3}. \]
Compute the power: \( 3^8 = 6561 \).
\[ S_8 = \frac{2(1 - 6561)}{-2} = \frac{-13120}{-2} = 6560. \]
Answer: \( S_8 = 6560 \).
GEOMETRIC PROGRESSION: PRACTICE
- Find \(x\), if it is known that the numbers \(-1, x + 2, x\), taken in the given order, form a geometric progression.
- The sum of the first five terms of a geometric progression is \(\frac 32\) greater than the sum of its first three terms. The fifth term of the progression is equal to its third term multiplied by 4. Find the fourth term of the progression, if it is known that its common ratio is positive.
- The sum of the first three terms of a geometric progression is 12, and the sum of the first six terms is -84. Find the third term.
- Three numbers, the third of which is 12, form a geometric progression. If 12 is replaced by 9, the resulting numbers form an arithmetic progression. Find the original numbers.
- Find four positive numbers such that the first three form an arithmetic progression, and the last three form a geometric progression. The sum of the first three numbers is 12, and the sum of the last three is 19.
- -1 or -4.
- 0.5.
- 16.
- 27, 18, 12 or 3, 6, 12.
- 2, 4, 6, 9.
Exit Ticket
The numbers 4, x, and 36 form a non-monotonic geometric progression. Find x.
Geometric Progression
Key questions:
- Which sequence is called a geometric progression?
- How does the common ratio affect the type of monotonicity?
- Which formulas allow calculations related to a geometric progression?
Warm-up
In the first line, write the first seven powers of two.
In the second line, find the sums of these powers.
What pattern do you notice?
Concept of a Geometric Progression
A numerical sequence is an ordered set of numbers in which each element is assigned its own index. The elements of a sequence are usually denoted by lowercase Latin letters with subscripts: \( a_1, a_2, a_3, \ldots \).
Let us consider several examples of numerical sequences:
- \( 2, 4, 8, 16, 32, \ldots \) — the sequence of powers of 2;
- \( 3, 6, 12, 24, 48, \ldots \) — each next element is twice the previous one;
- \( 1, -2, 4, -8, 16, \ldots \) — a sequence with alternating signs.
Task: Find the seventh element in each of the given sequences.
A geometric progression is a numerical sequence in which each next element is obtained from the previous one by multiplying by the same nonzero number. This number is called the common ratio of the geometric progression and is denoted by the letter q.
For example, in the sequence \[ 2, 6, 18, 54, \ldots \] each next element is obtained by multiplying the previous one by 3, therefore \( q = 3 \). The notation \( a_4 \) corresponds to the fourth element of the sequence, that is, \( a_4 = 54 \).
Task: Determine the common ratio of the geometric progression \( 5, 10, 20, 40, \ldots \) and find its seventh element.
The general term of a geometric progression is given by the formula:
\( a_n = a_1 \cdot q^{\,n-1} \)
Using this formula, one can find any term of the progression if its first term and common ratio are known.
Task: Using the formula for the general term, find the seventh element of a geometric progression with first term \( a_1 = 3 \) and common ratio \( q = 2 \).
The type of monotonicity of a geometric progression whose first term is positive depends on the common ratio as follows:
- if \( q > 1 \), the progression is increasing (each subsequent term is greater than the previous one);
- if \( 0 < q < 1 \), the progression is decreasing (each subsequent term is less than the previous one);
- if \( q < 0 \), the signs of the terms alternate (there is no monotonicity).
Task: Determine the type of monotonicity of a geometric progression whose first term is negative.
GEOMETRIC PROGRESSION: PRACTICE
- Place two numbers between 7 and 56 so that they form a geometric progression.
- Find the third term of a geometric progression if its common ratio is 3, and the sum of the first four terms is -40.
- Find the common ratio of an increasing geometric progression if the difference between its fifth and first terms is five times greater than the difference between its third and first terms.
- Find a decreasing geometric progression whose sum of the first three terms is 7 and whose product is 8.
- Find three positive numbers forming a geometric progression if their sum is 21, and the sum of their reciprocals is \( \frac{7}{12}\).
- In a geometric progression, the sum of the first and fifth terms is 51, and the sum of the second and sixth terms is 102. How many terms of this progression must be taken (starting from the first) so that their sum is 3069?
- 14 and 28.
- -9.
- 2.
- 4, 2, 1.
- 3, 6, 12.
- 10.
Exit Ticket
Write any 7 numbers that form a geometric progression. What property do the pairwise products of elements located symmetrically with respect to the central one have?
Differentiated Payments
Key Questions:
- What are the main parameters of a loan agreement?
- How is the loan repaid?
- What is a differentiated payment scheme?
Warm-Up
List all two-digit numbers that leave a remainder of 5 when divided by 12. How can you find their sum?
1. Loan Agreement and Repayment Scheme
Loan Agreement Parameters
When taking out a mortgage, the parties agree on the following main parameters:
- Loan Amount — the size of the loan;
- Term — the number of repayment periods (months);
- Interest Rate — the cost of using the loan;
- Repayment Scheme — the method of returning the debt to the bank.
The interest rate is usually stated as an annual rate. However, interest accrual and payment calculations are made per repayment period, most often monthly. Therefore, the annual rate must be converted to a rate per period. For example, if the annual rate is \(12\%\), the monthly rate is \( \dfrac{12\%}{12} = 1\% \). This means that each month interest is charged at \(1\%\) of the remaining principal.
Payment Structure
Each loan payment consists of two parts:
- interest charged on the remaining debt;
- the portion of principal repayment.
Interest decreases as the remaining debt decreases, and principal repayment depends on the chosen repayment scheme.
Consider an example. Let the annual interest rate be \(24\%\), the remaining principal at the beginning of the period be \(5000\) dollars, and the principal repayment for this period be \(1000\) dollars.
Convert the annual rate to a monthly rate:
\[ \frac{24\%}{12} = 2\% \text{ per month}. \]
Then the interest for the period will be:
\[ 5000 \cdot 0{,}02 = 100 \text{ dollars}. \]
The total payment for this period is the sum of the interest and the principal repayment:
\[ 100 + 1000 = 1100 \text{ dollars}. \]
Thus, under a differentiated repayment scheme, the payment amount in each period is determined by the current remaining debt and the fixed principal repayment amount.
It is convenient to organize calculations for the entire loan term in a table:
| Period | Remaining Debt |
Interest Charged |
Repayment Amount |
Payment for Period |
|---|---|---|---|---|
| 1 | 6000 | 120 | 1000 | 1120 |
| 2 | 5000 | 100 | 2000 | 2100 |
| 3 | 3000 | 60 | 3000 | 3060 |
Differentiated Payments
Under a differentiated scheme, the parties agree that in each period the same amount of principal is repaid.
As a result:
- the remaining debt decreases evenly;
- interest decreases each period;
- total payment gradually decreases.
Consider an example.
Loan: $10,000
Term: 4 months
Interest rate: 6% per year
Monthly rate: \[ \frac{6\%}{12} = 0{,}5\% = 0{,}005 \]
Principal repayment each month: \[ \frac{10\,000}{4} = 2\,500 \]
| Period | Remaining Debt |
Interest Charged |
Repayment Amount |
Payment for Period |
|---|---|---|---|---|
| 1 | 10 000 | 50 | 2 500 | 2 550 |
| 2 | 7 500 | 37,5 | 2 500 | 2 537,5 |
| 3 | 5 000 | 25 | 2 500 | 2 525 |
| 4 | 2 500 | 12,5 | 2 500 | 2 512,5 |
Note an important fact: the values in all columns form arithmetic progressions! Therefore, the total of all payments can be found:
- by direct addition;
- using the formula for the sum of an arithmetic progression.
\[ S = \frac{n(a_1 + a_n)}{2} = \frac{4(2550 + 2512{,}5)}{2} = 10\,125 \]
The overpayment for the loan will be only 1.25%:
\[ 10\,125 - 10\,000 = 125 \]
ARITHMETIC PROGRESSION: PRACTICE
- Find a three-digit number divisible by 45 whose digits form an arithmetic progression.
- The sum of the third and seventh terms of an arithmetic progression is 24, and their product is 128. Find the common difference of the progression.
- The second term of an arithmetic progression consisting of integers is 2. It is known that the sum of the squares of the third and fourth terms equals 4. Find the first term of the progression.
-
On December 15, 2026, a loan of 6 million is planned to be taken from a bank for 24 months.
The repayment conditions are as follows:
— On the 1st day of each month, the debt increases by 3% compared to the end of the previous month;
— From the 2nd to the 14th day of each month, a single payment is made to cover part of the debt;
— On the 15th day of each month, the debt must be reduced by the same amount compared to the 15th day of the previous month;
— By December 15, 2028, the loan must be fully repaid.
What is the total amount of payments in 2027? -
On December 15, 2026, a loan of 9 million is planned to be taken from a bank for 24 months.
The repayment conditions are as follows:
— On the 1st day of each month, the debt increases by r% compared to the end of the previous month;
— From the 2nd to the 14th day of each month, a single payment is made to cover part of the debt;
— On the 15th day of each month, the debt must be reduced by the same amount compared to the 15th day of the previous month;
— By December 15, 2028, the loan must be fully repaid.
Determine the interest rate if the total payments in 2027 amounted to 6,165 thousand. -
On December 15, 2026, a loan of A million is planned to be taken from a bank for 60 months.
The repayment conditions are as follows:
— On the 1st day of each month, the debt increases by 2% compared to the end of the previous month;
— From the 2nd to the 14th day of each month, a single payment is made to cover part of the debt;
— On the 15th day of each month, the debt must be reduced by the same amount compared to the 15th day of the previous month;
— By December 15, 2031, the loan must be fully repaid.
Determine the loan amount if the total payments in 2031 amounted to 1,356 thousand.
- 135.
- 2 or -2.
- 4.
- 3,318,000.
- 2%.
- 6,750,000.
Exit Ticket
$10,000 is borrowed for 5 months at an annual rate of 12% with differentiated payments. Determine the payment amount for the second period.
Sum of an Arithmetic Progression
Key questions:
- What property do three consecutive terms have?
- Which method allows us to quickly compute the sum of consecutive terms?
- How can an arithmetic progression be reconstructed using equations?
Warm-up
Find the sum of all integers from 1 to 1000.
Characteristic Property of an Arithmetic Progression
Three consecutive terms of an arithmetic progression have an important property: the middle term equals the arithmetic mean of its two neighbors.
\[ a_k = \frac{a_{k-1} + a_{k+1}}{2}. \]
This property makes it possible to form equations and reconstruct the terms of a progression from incomplete data.
Pairwise Summation Method
To quickly compute the sum of the first \(n\) terms of an arithmetic progression, the pairwise summation method is used.
The first and last terms, the second and the second-to-last terms, and so on, form pairs with the same sum:
\[ a_1 + a_n = a_2 + a_{n-1} = \ldots \]
There are exactly \( \dfrac{n}{2} \) such pairs if \(n\) is even, and \( \dfrac{n-1}{2} \) pairs plus one middle term if \(n\) is odd.
This method is the basis of the formula for the sum of an arithmetic progression.
Formula for the Sum of an Arithmetic Progression
The sum of the first \(n\) terms of an arithmetic progression equals the product of the number of terms and the arithmetic mean of the first and the last terms:
\[ S_n = \frac{n(a_1 + a_n)}{2}. \]
This formula is especially convenient when the extreme terms of the progression are known.
Example
Find the sum of the first twelve terms of an arithmetic progression if it is known that \( a_2 = 8 \) and \( a_{10} = 40 \).
We use the formula for the general term of an arithmetic progression:
\[ a_n = a_1 + (n - 1)d. \]
From the given conditions we obtain the system:
\[ \begin{cases} a_1 + d = 8, \\ a_1 + 9d = 40. \end{cases} \]
Subtract the first equation from the second:
\[ 8d = 32 \quad \Rightarrow \quad d = 4. \]
Substituting the value of the common difference into the first equation, we get:
\[ a_1 = 8 - 4 = 4. \]
Now find the twelfth term of the progression:
\[ a_{12} = a_1 + 11d = 4 + 44 = 48. \]
Use the formula for the sum of the first \(n\) terms of an arithmetic progression:
\[ S_{12} = \frac{12(a_1 + a_{12})}{2} = 6 \cdot (4 + 48) = 312. \]
Answer: \( S_{12} = 312 \).
ARITHMETIC PROGRESSION: PRACTICE
- The second and fourth terms of an arithmetic progression are 6 and 16 respectively. Find the fifth term of the progression.
- The sum of the fourth and sixth terms of an arithmetic progression is 14. Find the sum of the first nine terms of the progression.
- Find the sum of the first twenty terms of an arithmetic progression if it is known that the sum of the third, seventh, fourteenth, and eighteenth terms equals 10.
- Find the sum of all three-digit numbers divisible by three.
- An arithmetic progression has 20 terms. The sum of the terms in even positions is 250, and in odd positions — 220. Find the tenth term of the progression.
- Solve the equation in which \(x\) is a natural number: \[\dfrac{x - 1}{x^2} + \dfrac{x - 2}{x^2} + \ldots + \dfrac{1}{x^2} = \dfrac{7}{15}.\]
- 21.
- 63.
- 50.
- 165150.
- 22.
- \(x = 15\).
Exit Ticket
It is known that the sum of the first \(n\) terms of an arithmetic progression equals \(120\), and the first and last terms of this sum are \(5\) and \(35\). Find \(n\).
Arithmetic Progression
Key Questions:
- What is a numerical sequence?
- Which sequence is called an arithmetic progression?
- What formulas allow calculations related to arithmetic progressions?
Warm-up
A snail crawls from one tree to another. Each day it covers a distance that is the same amount longer than the previous day. It is known that on the first and last days the snail covered a total of 10 meters. Determine how many days the snail took to cover the entire distance, if the distance between the trees is 150 meters.
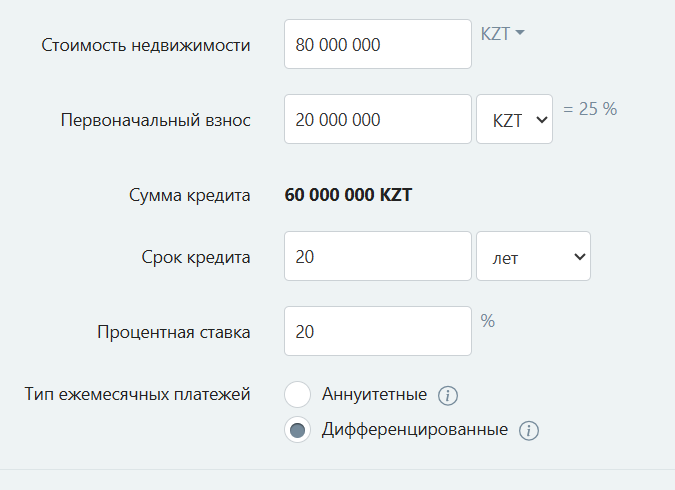
What do you see in this picture?
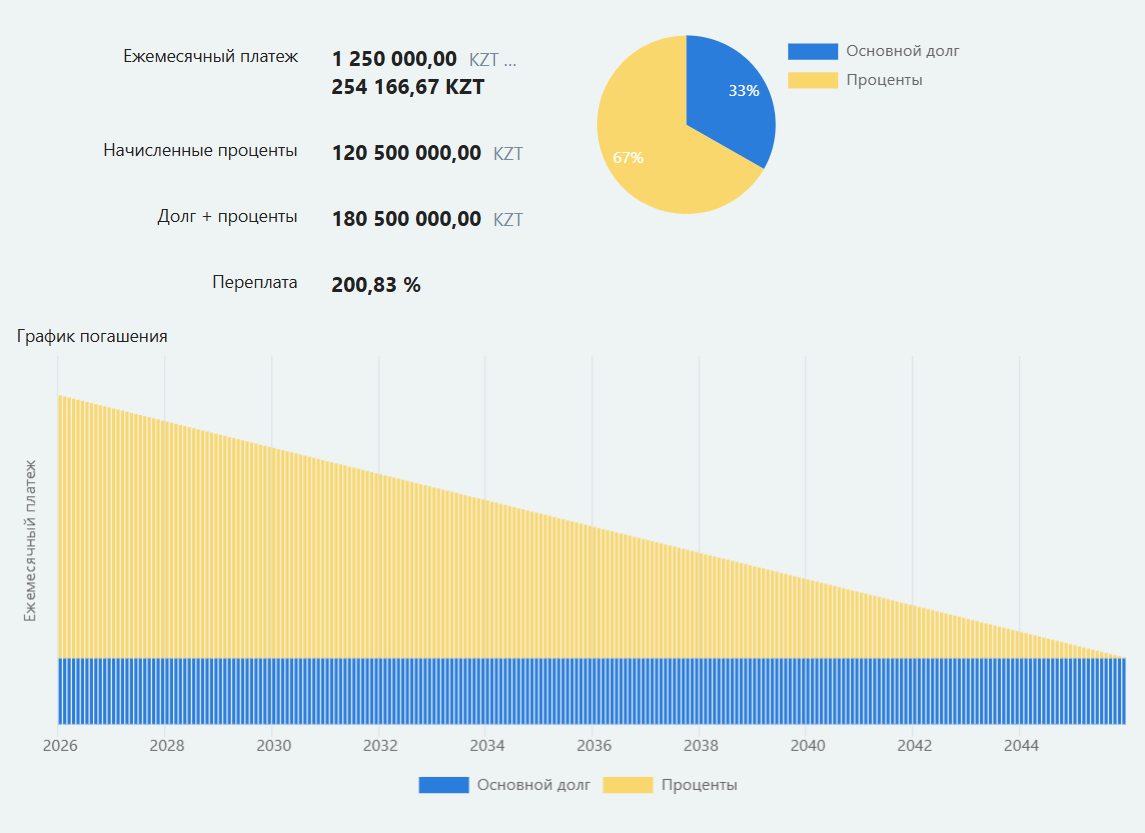
What could be the conditions of this agreement?
Concept of Arithmetic Progression
Numerical sequence — an ordered set of numbers, in which a rule for generating all elements is specified.
Examples of different numerical sequences:
- \(1, 2, 3, 4, 5, \ldots\) — sequence of natural numbers;
- \(1, 1, 2, 3, 5, 8, \ldots\) — Fibonacci sequence, where each element from the third onward is the sum of the two previous elements;
- \(1, 4, 1, 5, 9, \ldots\) — digits after the decimal point of \( \pi \), with no obvious pattern.
Task: Find the fifteenth element in each of the sequences listed above.
Arithmetic progression — a sequence in which each next element differs from the previous one by the same number.
Elements of a sequence are usually denoted by lowercase Latin letters with subscripts indicating the position of the number in the list.
For example, in the progression \[1, 4, 7, 10, 13, \ldots\] the notation \(a_3\) refers to the third number in this list, that is \(a_3 = 7\).
The number by which consecutive elements of a progression differ is called its common difference and is denoted by d. In our example, \(d = 3\).
Task: Find the fifteenth element of this progression.
The general term of an arithmetic progression can be described by the following formula:
\( a_n = a_1 + (n - 1)d \)
Task: Use this formula to find the fifteenth element of the progression above.
ARITHMETIC PROGRESSION: PRACTICE
- Is the sequence \(6, 9, 12, 15, \ldots\) an arithmetic progression? Find its common difference.
- Find the eighth term of the progression: \(10, 16, 22, \ldots\)
- Find n if \(a_1 = 5\), \(d = 3\), \(a_n = 65\).
- Write the formula for the general term of the progression: \(−2, 1, 4, 7, \ldots\)
- Yes, d = 3
- 52
- n = 21
- \(a_n = -2 + (n - 1) \cdot 3\)
Exit Ticket
What pattern does this sequence follow: \(1, 2, 4, 7, 11, 16, 22, \ldots\)?